Why Doesn’t Music Get Boring With Only 12 Notes?

I know what you’re thinking:

“Why doesn’t it get boring?”

Some have taken an a mathematical approach to this question. Although these answers demonstrate a raw numerical reason, they offer little musical insight.

The problem is that their premise — “only 12 notes” — is a lie.

The Objection vs. The Octaves

You respond:

“But wait! The piano repeats the same 7 white keys and 5 black ones, so there are 12 notes.”

That may be true, but saying there’s only 12 pitches assumes that octave they’re played in makes no difference. If all the notes in a melody are transposed to the same octave, that’s true.[1. Well, true-ish. Interesting stuff can happen when you transpose melodies to the extremes of instruments’ ranges, where pitch discrimination becomes more difficult. See, for instance, the opening contrabassoon solo in Ravel’s Piano Concerto for the Left Hand.] But if you transpose the notes of a melody to different octaves, you may retain a flavor of the melody but it sounds distinctly different.

Here’s a video of how these distinctions play out in “Ode to Joy”:

But, for the moment, let’s play along. Let’s say we can call all octaves as equal. There are still more than 12 notes.

At this point, you may insist:

“From where are you getting these other pitches?”

From the 5-line staff.

Enter the Staff

Unlike the keyboard, the staff does not have 12 unique positions.

It has 7 basic pitches that can be modified not only with sharps and flats, but also with double-sharps, double-flats, and more esoteric constructions.[2. See examples from Alkan’s op. 39, no. 10 and Reger’s op. 49 no. 2.] If you count just the 3 basic positions of the 7 notes, that yields 21 pitches.[3. Incidentally, this accidental system is also how the modern harp works.] If you count double accidentals, that yields 35.

“But don’t many of those pitches sound the same?”

Sometimes. But we know there are instruments and ensembles who regularly distinguish between them.[4. For instance, string quartets, choirs, brass ensembles, etc.] Even for instruments that cannot, the staff reveals something deeper than what an oscilloscope or perfect pitch can identify.

It shows that context matters.

Just Like High School

No pitch exists in isolation.[5. Apart from some vary rare exceptions.] Though A-flat and G-sharp may seem the same alone, they never sound identical in tonal music, because different spellings suggest different behaviors and contexts.

Like cliché high schoolers, they have those in their clique, those with whom they occasionally interact, and those whom they avoid at all costs. For instance, A-flat is often around E-flat but rarely around E-natural, whereas G-sharp and E are good buddies.

Even a single pitch has multiple potential contexts, each with a different flavor:

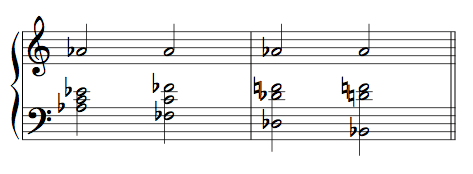
The soprano A-flat in example 2 is clearly same frequency, but the chord changes underneath it alter its meaning.

A Tradition of Puns and Rhymes

Far more than the raw statistical possibilities, an understanding of these multiple meanings — these puns and rhymes[6. “Shifting roles” is another good way to describe it.] — have given composers an easy way to keep things fresh while maintaining continuity.

Haydn was a master of these games. Take, for instance, his Piano Sonata Hob. XVI/1:

The opening three measures immediately demonstrate that a note in one context (C in C-E-G) feels totally different in another (C in C-F-A). Haydn helps you feel that shift the same way I did in example 2 — by having the note in question in the top voice.[7. He makes the even stronger by starting and ending the upward gesture on that same pitch. 6/12 pitches in the soprano of bars 1-3 are that C, and the Cs sit on prominent real estate.]

That little trifle pales to what Haydn does when he repeats the opening melody a third time (0’56, after the repeat). Previously that melody had been all smiles and sunshine, but here it feels doubly foreign. Not only has Haydn transposed it to the pitch level of the dominant, but also, instead of G major, he uses G minor.

Both these changes demonstrate what I mean by musical puns and reveal why they are effective. G minor is a lot like G major. Transposition aside, the opening melody and the one after the repeat are almost the same. Yet in the context of hearing twice both the original melody and the establishment of G major, these changes make the familiar sound new.

The Elegant Road

It’s these kinds of games composers have in mind when they’re trying to make sure the 12 or 21 or 35 pitches don’t get boring.

Because of their elegance, these games free composers who seeking new combinations from having to look up “Note Row Permutation no. 6,345,721,463” — and then work by the trial[8. This would be more than a trial. This would be a Sisyphean punishment.] and error to find which successions sounds good.

And for that fact, composers everywhere and I are grateful.

Notes